calculus - help?

[deadtom]

I was hoping someone could give me some guidance on a calculus problem i cant figure out how to do..

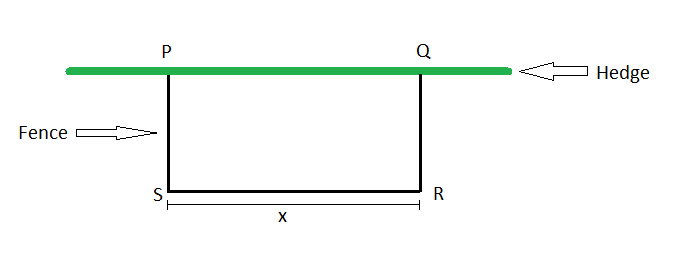
A farmer has length of electric fence that is 500m long. He uses it to enclose a rectangular grazing area on three sides, the fourth side being a fixed hedge. Find the maximum area he can enclose.

This is the simple diagram we were given.




I assume that the way to do it is to treat the short sides as 'y' and find an equation in the form of y = something x somethingsomething, which differentiates to a quadratic which can then be used to find the turning point co-ordinates, then find which is the maximum, the co ordinates of which will correspond to the lengths of x and y that will give the largest area inside the fence?

or am i way off?

and all i have so far is that PS = QR, so call this value y, so y = 250-(x/2)

help?

[Liszt]

deadtom said:

I was hoping someone could give me some guidance on a calculus problem i cant figure out how to do..

A farmer has length of electric fence that is 500m long. He uses it to enclose a rectangular grazing area on three sides, the fourth side being a fixed hedge. Find the maximum area he can enclose.

This is the simple diagram we were given.




I assume that the way to do it is to treat the short sides as 'y' and find an equation in the form of y = something x somethingsomething, which differentiates to a quadratic which can then be used to find the turning point co-ordinates, then find which is the maximum, the co ordinates of which will correspond to the lengths of x and y that will give the largest area inside the fence?

or am i way off?

and all i have so far is that PS = QR, so call this value y, so y = 250-(x/2)

help?

if a = area and x and y are sides of area

a=x*y

with a length of 500m = x + 2y (2 sides)

x+2y=500

Rearranging gives
-2y=x-500
y=-x/2 +(250)
substituting back into original

a=x(x/2 +250)
a=(x^2)/2 + 250x
Integrating to find the maxima gives

(2x+500)/2
=x+250

so x is maximum at 250 which makes max area 31250

[Eric Mc]

If I was the farmer, I'd hire a fencing contractor.

[andrew]

you differentiated rather than integrated in the middle, and lost a minus sign

but fiddled the minus sign for the correct answer

[LordGrover]

Eric Mc said:

If I was the farmer, I'd hire a fencing contractor.

Were I the farmer I'd be too tight to spend dosh on a contractor. I've already got the fence, hedge and field so I'd just go out and do it. Maybe pace it out once it's done.
Then I'd drink cider and eat cheese.

[Liszt]

andrew said:

you differentiated rather than integrated in the middle, and lost a minus sign

but fiddled the minus sign for the correct answer

It's been a decade and a half since I did this so give me a break! I knew what I meant

[Simpo Two]

I make it anywhere between 498m2 and 27,777.775m2... but I'm a string and pencil man.

[deadtom]

thanks chaps.

my friend who is better at this than I also got the result of x = 250, so i'll get him to explain it to me in words of one syllable tomorrow :P

[Ultuous]

First time I've had to do this for over a decade, but here goes...

Find 'y' (it's got to be the length of the tape that hasn't been used by 'x', halved to make the two sides:

y=(500-x)/2

Work out the area, substituting y for x using the above:

A = x*y = x*(500-x)/2 = (500x-x^2)/2 = 250x-x^2/2

Differentiate to find the 'top' of the curve:

dA/dX = 250-2x/2 = 250-x = 0 --> x = 250!

Check this is a maximum by differentiating again:

dA2/dx2 = -1 - not surprising really - the A is going to be zero but increasing from x=0, and back at zero for x=500, so there can be only one maximum!

ETA: Please don't take this to be patronising, but if you're going to be doing a fair bit of this, I'd recommend swatting up on relatively basic algebra/ geometry before worrying too much about the calculus...

I saw too many people (myself included sometimes) becoming unstuck during my engineering degree by attempting to 'gloss over' the relatively simple maths that they just needed to spend a bit of time getting their head around or asking for help on!

Edited by Ultuous on Thursday 19th January 19:45

[andrew]

anyway, why does the area have to be a rectangle ?

a semi-circle would be truly optimal

[deadtom]

Ultuous said:

maths stuff

yeah thats the method i had in my head, just couldnt quite see what exactly to differentiate to get the right answer.

thanks though (and you too liszt), and im usually ok with calculus but ive only just gone back to uni after a month off over christmas, so naturally ive forgotten everything i learned in the first term.

also in my defence, im doing a foundation year after being out of education for 6 years, so its all new to me.

[kiteless]

deadtom said:

This is the simple diagram we were given.

Maximum land usage would be S-R (x-axis) = 300m x Q-R (y-axis) = 100m. This yields 30,000m2. Broadening or shortening either axes from this results in less land usage (e.g. an x-axis of 437.50m and a y-axis of 31.25m yields 13,600m2). This, of course, assumes opposing sides of the area to be of equal length.

[Otispunkmeyer]

Ultuous said:

First time I've had to do this for over a decade, but here goes...

Find 'y' (it's got to be the length of the tape that hasn't been used by 'x', halved to make the two sides:

y=(500-x)/2

Work out the area, substituting y for x using the above:

A = x*y = x*(500-x)/2 = (500x-x^2)/2 = 250x-x^2/2

Differentiate to find the 'top' of the curve:

dA/dX = 250-2x/2 = 250-x = 0 --> x = 250!

Check this is a maximum by differentiating again:

dA2/dx2 = -1 - not surprising really - the A is going to be zero but increasing from x=0, and back at zero for x=500, so there can be only one maximum!

ETA: Please don't take this to be patronising, but if you're going to be doing a fair bit of this, I'd recommend swatting up on relatively basic algebra/ geometry before worrying too much about the calculus...

I saw too many people (myself included sometimes) becoming unstuck during my engineering degree by attempting to 'gloss over' the relatively simple maths that they just needed to spend a bit of time getting their head around or asking for help on!

Edited by Ultuous on Thursday 19th January 19:45

indeed

the other day I tried to differentiate between two points... before realising you do this for integration for finding area under a curve!

If you don't use it you lose it!

is it that if D2A/dx2 < 0 its a max point, > 0 a min point and = 0 it might be an inflexion?

[deadtom]

Otispunkmeyer said:

is it that if D2A/dx2 < 0 its a max point, > 0 a min point and = 0 it might be an inflexion?

correct. if the second derivative has a negative value then it's a decreasing gradient (ie, the top of a curve) so you have a maxima, and vice versa when the second derivative is positive.


















right? =/

[tank slapper]

kiteless said:

Maximum land usage would be S-R (x-axis) = 300m x Q-R (y-axis) = 100m. This yields 30,000m2. Broadening or shortening either axes from this results in less land usage (e.g. an x-axis of 437.50m and a y-axis of 31.25m yields 13,600m2). This, of course, assumes opposing sides of the area to be of equal length.

So how about when x=250 and y=125? As posted a couple of times above, complete with method.

[tank slapper]

Otispunkmeyer said:

indeed

the other day I tried to differentiate between two points... before realising you do this for integration for finding area under a curve!

If you don't use it you lose it!

is it that if D2A/dx2 < 0 its a max point, > 0 a min point and = 0 it might be an inflexion?

With quadratics, you don't really need to do that though since they only have one stationary point and it won't be an inflection. If the x^2 coefficient is positive, it will be a minimum and if it is negative it will be a maximum. The 2nd derivative test is useful for higher polynomials though.

[Ultuous]

deadtom said:

also in my defence, im doing a foundation year after being out of education for 6 years, so its all new to me.

No need for a defence - the only reason I say make sure you understand ALL of the maths is that you either have the understanding of a mathematical concept or you don't - I honestly think that if you 'sort of' understand anything mathematical it hasn't fully clicked - yet!

I lost the plot on my degree when it came to Laplace Transforms and other similiarly 'advanced' maths - I was probably down the Union when they were explained to me/ I should have been making sure they were explained to me properly by someone...

From then on in I was destined to struggle to a 2:2 when I should really have been capable of higher (I still have the occasional nightmare that I'm back in the exam room for my finals feeling completely clueless, despite it being last millenium!)... A couple of hours here and there making sure I understood exactly what was going on would probably have saved a lot of time and stress 'bodging' my studies for the last couple of years!... Just stick at it and take the attitude that if you don't understand something it's because you need to be shown it properly and I'm sure you'll be fine!

[Jinx]

andrew said:

anyway, why does the area have to be a rectangle ?

a semi-circle would be truly optimal

I like your thinking.
so pi*R = 500 - as in semi circle circumference = 500
Rearranging for R = 500/pi
Area of semi circle = .5*pi*(500/pi)^2 = 39788.73577 (or there abouts)
Nice.

[Simpo Two]

Jinx said:

so pi*R = 500 - as in semi circle circumference = 500
Rearranging for R = 500/pi
Area of semi circle = .5*pi*(500/pi)^2 = 39788.73577 (or there abouts)

Now that's maths I can understand!

[PugwasHDJ80]

Jinx said:

andrew said:

anyway, why does the area have to be a rectangle ?

a semi-circle would be truly optimal

I like your thinking.
so pi*R = 500 - as in semi circle circumference = 500
Rearranging for R = 500/pi
Area of semi circle = .5*pi*(500/pi)^2 = 39788.73577 (or there abouts)
Nice.

i did my A-level maths project on this (well over 15 years ago now)

can't remember the details, but created a formula that proved for any regular shape where the internal angles added up to 360degrees, the most efficient use of space was proven by the number of corners tending to infinity- ie a circle (which is an infinite number of tiny corners).

Had another formula for irregular shapes, but it didn't actually "prove" anything, just showed a tendency. it worked off proving that the most efficient space was given when all the lengths of the "sides" tended to be the same length...