Maths Puzzle

[Alex]

This was originally in Acorn User magazine many years ago.

Find a 9-digit integer that is exactly divisible by 9.
Now remove the 9th digit to leave an 8-digit integer that is exactly divisible by 8.
Now remove the 8th digit to leave an 7-digit integer that is exactly divisible by 7.
And so on, down to a 1-digit integer that is obviously divisible by 1.

What is the 9-digit number? Is there more than one answer?

[zippy3x]

there are 2492 number that fit that bill

the last of which is 987654564

[Road2Ruin]

zippy3x said:

there are 2492 number that fit that bill

the last of which is 987654564

and the first is 102456243


Maybe.

[zippy3x]

Road2Ruin said:

and the first is 102456243


Maybe.

According to my (very hastily written program) the first is 102000564

[Road2Ruin]

I did say maybe. Yes I missed that one....

[zippy3x]

and eight others

[130R]

I'm sure there is a better way of doing it but (apologies for formatting but the code tags don't seem to work):

int count = 0;
for (int i = 100000000; i < 999999999; i++) {
int div = 9;
int temp = i;
do {
if (temp % div == 0) {
div--;
temp = (temp / 10);
} else break;
} while (div > 0);
if (div == 0) count++;
}

[Road2Ruin]

sorry, forgot to carry the 1

[Tyre Smoke]

To be honest, you lost me at 'integer'. I thought that was a car made by Honda. From there it was all downhill.

[bishbash]

I agree with zippy

[zippy3x]

Here's my code

DateTime start = DateTime.Now;
int count = 0;
for (int i = 100000000; i < 999999999; i++)
{
if (i % 9 == 0)
{
int n = i / 10;
if (n % 8 == 0 && ((n /= 10) % 7 == 0) && ((n /= 10) % 6 == 0) && ((n /= 10) % 5 == 0) &&
((n /= 10) % 4 == 0) && ((n /= 10) % 3 == 0) && ((n /= 10) % 2 == 0))
{
Console.WriteLine(i.ToString());
count++;
}
}
}

TimeSpan duration = DateTime.Now.Subtract(start);
Console.WriteLine(count.ToString());
Console.WriteLine("duration - " + duration.ToString());

Duration 5.95 seconds - quickly hacked and optimised for speed

anyone got a working BBC or electron? I'd love to know how long that would take on a 30 year old machine

[Alex]

Damn. Forgot to mention, the digits from 1 to 9 can only appear once each in the number.

[tribbles]

zippy3x said:

anyone got a working BBC or electron? I'd love to know how long that would take on a 30 year old machine

I've got 7 - but I would probably not write it in C#

[jammy_basturd]

Alex said:

Damn. Forgot to mention, the digits from 1 to 9 can only appear once each in the number.

Luckily Microsoft made a brilliantly realistic emulator.

They called it Vista.

[zippy3x]

Alex said:

Damn. Forgot to mention, the digits from 1 to 9 can only appear once each in the number.

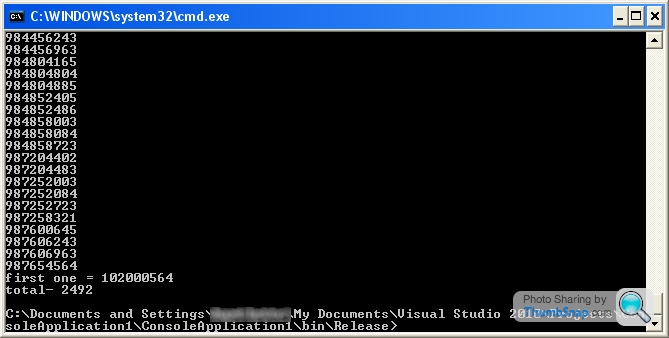
Tease....

Ok - with the new criteria it's down to 121

However i will pre-empt your next post and tell you that when the digits 0 to 9 can only appear one it goes down to 4

381654720
381654729
783204165
801654723

[Alex]

zippy3x said:

Tease....

Ok - with the new criteria it's down to 121

However i will pre-empt your next post and tell you that when the digits 0 to 9 can only appear one it goes down to 4

381654720
381654729
783204165
801654723

381654729 was the answer I was looking for, and is the only solution without using zero.

I wrote a BASIC program to solve it on my mate's Dragon 32. I recall it ran for around 30 minutes before finding the solution.

[Some Gump]

Lightning Bolt!

[tribbles]

zippy3x said:

Tease....

Ok - with the new criteria it's down to 121

However i will pre-empt your next post and tell you that when the digits 0 to 9 can only appear one it goes down to 4

381654720
381654729
783204165
801654723

I've done my own version (in C#)...

C:\stprojects\tmp\NumberCrunch\NumberCrunch\bin\Debug>NumberCrunch.exe
381654720
381654729
783204165
801654723
Count: 4
duration - 00:00:00
Yes, I am running debug. Yes, it did take 0 seconds.

The thing is you've got to think about it in reverse. My code starts with the first two digits, and makes sure that they're different, and the number's even. All other combinations after this can be ignored. It then adds the third number, checks it's different, and makes sure that it's divisible by 3. And so on.

For the 2nd, 4th, 6th and 8th numbers, they need to be even - so it just starts at 0, and increments by 2.

Here's the code:

DateTime start = DateTime.Now;
int count = 0;

for (int a = 1; a < 10; a++)
{
for (int b = 0; b < 10; b += 2)
{
if (a == b)
continue;

for (int c = 0; c < 10; c++)
{
if ((c == a) || (c == b))
continue;
if (((a + b + c) % 3) != 0)
continue;

for (int d = 0; d < 10; d += 2)
{
if ((d == a) || (d == b) || (d == c))
continue;
if (((c * 10 + d) & 3) != 0)
continue;

for (int e = 0; e < 10; e += 5)
{
if ((e == a) || (e == b) || (e == c) || (e == d))
continue;

for (int f = 0; f < 10; f += 2)
{
if ((f == a) || (f == b) || (f == c) || (f == d) || (f == e))
continue;

if (((a + b + c + d + e + f) % 3) != 0)
continue;

for (int g = 0; g < 10; g++)
{
if ((g == a) || (g == b) || (g == c) || (g == d) || (g == e) || (g == f))
continue;
if (((a * 1000000 + b * 100000 + c * 10000 + d * 1000 + e * 100 + f * 10 + g) % 7) != 0)
continue;

for (int h = 0; h < 10; h++)
{
if ((h == a) || (h == b) || (h == c) || (h == d) || (h == e) || (h == f) || (h == g))
continue;
if (((f * 100 + g * 10 + h) & 7) != 0)
continue;

for (int i = 0; i < 10; i++)
{
if ((i == a) || (i == b) || (i == c) || (i == d) || (i == e) || (i == f) || (i == g) || (i == h))
continue;
if (((a + b + c + d + e + f + g + h + i) % 9) != 0)
continue;

Console.WriteLine(string.Format("{0}{1}{2}{3}{4}{5}{6}{7}{8}", a, b, c, d, e, f, g, h, i));
count++;
}
}
}
}
}
}
}
}
}

TimeSpan duration = DateTime.Now.Subtract(start);
Console.WriteLine(string.Format("Count: {0}", count));
Console.WriteLine("duration - " + duration.ToString());

I nicked your timespan code - easier than writing my own.

Each check to see if it's divisible by <n>, I've used mathematical trickery where possible.

ETA: I found a slight bug, which I corrected here before testing it, and it came up with other answers. I'll correct it when it's done, but hopefully the idea of how to solve this has been put across.

Edited again: I found the bug, and it's now producing the same 4 results, albeit a bit faster I've corrected the code.

Edited by tribbles on Tuesday 22 February 16:19

Edited by tribbles on Tuesday 22 February 16:22

[Alex]

OK, we know the answer. Let's change this to a coding challenge!

I propose the following categories:

• Most elegant
• Shortest
• Fastest
• Daftest

You can use any language. I'll have a go myself.

No doubt some LISP expert will come along with a single line solution...

[zippy3x]

Alex said:

OK, we know the answer. Let's change this to a coding challenge!

I propose the following categories:

• Most elegant
• Shortest
• Fastest
• Daftest

You can use any language. I'll have a go myself.

No doubt some LISP expert will come along with a single line solution...

I'll have a go at Most Elegant, Shortest and Fastest

Console.WriteLine("381654729");

anyone do better?